Простые способы и формулы для определения площади фигуры

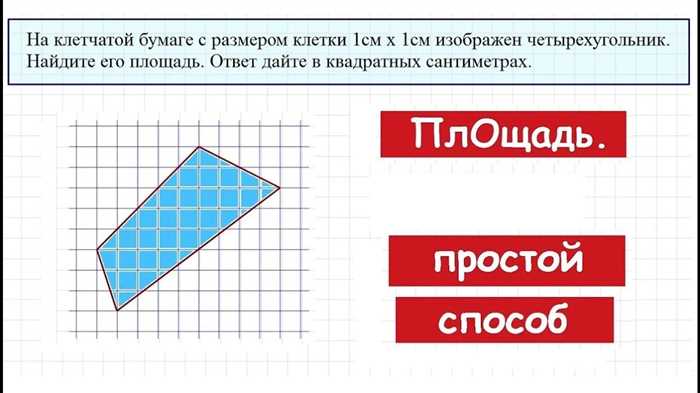
Геометрические фигуры могут иметь различные формы и размеры, и для вычисления их площади существуют разные способы. Например, площадь прямоугольника можно найти, зная его длину и ширину, и она равна произведению этих двух величин. Такое же правило справедливо и для квадрата, площадь которого также измеряется в квадратных единицах.

В математике существуют формулы для нахождения площади разных фигур. Например, для треугольника можно использовать формулу Герона, которая позволяет вычислить площадь треугольника, зная длины его сторон. Для прямоугольного треугольника площадь равна половине произведения длины катета и высоты, которая проведена к гипотенузе.

Еще одной характеристикой фигуры, которая поможет найти ее площадь, является высота. Например, для трапеции площадь равна половине суммы длины оснований, умноженной на высоту. А для круга площадь равна произведению квадрата радиуса на число Пи.

Таким образом, существует множество разных способов нахождения площади фигур, и для каждой из них есть своя формула. Зная эти формулы и условия, которым должна удовлетворять фигура, можно легко вычислить ее площадь и получить численную характеристику всей ограниченной поверхности.

Как найти площадь всей фигуры зная только площади всех её частей

Для вычисления площади всей фигуры, когда известны площади всех её частей, можно использовать различные способы и формулы. В данном разделе мы рассмотрим несколько простых методов.

Один из способов заключается в суммировании площадей всех частей фигуры. Если фигура разделена на несколько частей, то площадь всей фигуры будет равна сумме площадей этих частей.

Например, если фигура состоит из трех частей — квадрата, прямоугольника и треугольника, то площадь всей фигуры будет равна сумме площадей этих трех частей.

Если известны площади всех частей фигуры, то можно использовать формулу для вычисления площади каждой части и затем сложить полученные значения.

Например, для вычисления площади треугольника можно использовать формулу: площадь треугольника = (основание * высота) / 2. Зная площадь треугольника и значения основания и высоты, можно вычислить площадь треугольника.

Таким же образом можно вычислить площади других геометрических фигур, таких как прямоугольник, круг, эллипс, трапеция и т.д. Для каждой фигуры существует своя формула для вычисления площади.

Если фигура состоит из нескольких частей, которые не пересекаются, то площадь всей фигуры будет равна сумме площадей этих частей.

Например, если фигура состоит из двух прямоугольников, то площадь всей фигуры будет равна сумме площадей этих двух прямоугольников.

Если фигура состоит из нескольких частей, которые пересекаются, то для вычисления площади всей фигуры может потребоваться использование более сложных формул и методов.

Важно помнить, что для вычисления площади всей фигуры необходимо знать площади всех её частей. Если площади частей фигуры неизвестны, то найти площадь всей фигуры будет невозможно.

Таким образом, чтобы найти площадь всей фигуры, зная только площади всех её частей, необходимо использовать соответствующие формулы для вычисления площади каждой части и затем сложить полученные значения.

Спасибо за внимание!

Площадь прямоугольного параллелепипеда

Площадь поверхности прямоугольного параллелепипеда можно найти с помощью формулы:

S = 2 * (a * b + a * c + b * c),

где S — площадь поверхности, a — длина, b — ширина, c — высота параллелепипеда.

Все величины измеряются в одинаковых единицах измерения, например, в квадратных сантиметрах или квадратных метрах.

Чтобы разобраться в этом способе вычисления площади, давайте рассмотрим пример. Предположим, у нас есть прямоугольный параллелепипед с длиной 5 см, шириной 3 см и высотой 4 см. Чтобы найти площадь поверхности, мы подставляем значения в формулу:

S = 2 * (5 * 3 + 5 * 4 + 3 * 4) = 2 * (15 + 20 + 12) = 2 * 47 = 94.

Таким образом, площадь поверхности прямоугольного параллелепипеда равна 94 квадратным сантиметрам.

Площадь прямоугольного параллелепипеда является характеристикой его поверхности. Эта величина поможет нам ответить на вопрос, сколько материала потребуется для покрытия всей поверхности фигуры.

Если у вас есть прямоугольный параллелепипед, и вам требуется найти площадь одной из его частей, то можно использовать ту же формулу, но учитывать только те поверхности, которые вам интересны.

Например, если вам нужно найти площадь одной из боковых поверхностей параллелепипеда, то в формуле нужно учесть только две параллельные поверхности, которые разделены углом 90 градусов.

Таким образом, площадь боковой поверхности прямоугольного параллелепипеда равна a * c, где a — длина, c — высота параллелепипеда.

В математике площадь прямоугольного параллелепипеда является одним из способов измерения его поверхности. Эта величина измеряется в квадратных единицах, например, в квадратных сантиметрах или квадратных метрах.

Теперь, когда вы знаете, как найти площадь прямоугольного параллелепипеда, вы можете легко решать задачи по этой теме. Если у вас возникли вопросы, не стесняйтесь задавать их на сайте onlinemschool.ru. Спасибо за внимание!

Что такое площадь

Площадь фигуры может быть измерена в различных единицах, таких как квадратные метры, квадратные сантиметры, квадратные дюймы и т.д. Чтобы вычислить площадь фигуры, пользователь должен знать длину или размеры разделенной фигуры, для которой требуется вычислить площадь.

В геометрии существует множество способов вычисления площади различных фигур. Некоторые из них включают формулы для вычисления площади прямоугольного треугольника, круга, эллипса, квадрата, параллелограмма, трапеции, цилиндра, конуса, шара и других геометрических фигур.

Например, площадь прямоугольника вычисляется как произведение его длины и ширины, площадь круга — как произведение числа пи на квадрат радиуса, площадь треугольника — по формуле Герона, а площадь трапеции — как сумма площадей двух прямоугольных треугольников, находящихся между основаниями.

Зная формулы для вычисления площади различных фигур, можно разобраться с площадью любой фигуры. Сайт onlinemschool.ru предоставляет курс по математике, который поможет вам разобраться с площадью и другими геометрическими характеристиками фигур. Спасибо за внимание!

Площадь конуса

Если известны длина окружности основания и длина образующей, то площадь конуса можно найти по формуле:

S = (π * r^2) + (π * r * l)

где S — площадь конуса, π — число Пи (приближенно равно 3.14), r — радиус основания конуса, l — длина образующей конуса.

Если известны только радиус основания и высота конуса, то площадь конуса можно найти по формуле:

S = π * r * (r + l)

где S — площадь конуса, π — число Пи (приближенно равно 3.14), r — радиус основания конуса, l — высота конуса.

Также существует численная формула для нахождения площади конуса, которая основана на формуле Герона для треугольника. Она позволяет найти площадь конуса, зная радиус основания и высоту конуса:

S = π * r * (r + √(r^2 + h^2))

где S — площадь конуса, π — число Пи (приближенно равно 3.14), r — радиус основания конуса, h — высота конуса.

Зная эти формулы, пользователь может легко найти площадь конуса, зная необходимые величины. Поможет также использование онлайн-калькуляторов и специальных программ, которые могут автоматически рассчитать площадь конуса по заданным параметрам.

Важно помнить, что площадь конуса измеряется в квадратных единицах, так как это величина, которая находится путем измерения площадей различных частей фигуры и их суммирования. Некоторые измерения, такие как длина окружности, могут быть выражены в других единицах, но площадь всегда будет выражена в квадратных единицах.

Спасибо за внимание! В следующем разделе мы рассмотрим другую фигуру и способы вычисления ее площади.

Площадь

Площадь прямоугольника

Для нахождения площади прямоугольника необходимо знать его длину и ширину. Площадь прямоугольника равна произведению его длины на ширину.

Площадь квадрата

Площадь квадрата можно найти, зная длину его стороны. Площадь квадрата равна квадрату длины его стороны.

Площадь треугольника

Для нахождения площади треугольника необходимо знать его высоту и основание. Площадь треугольника равна половине произведения его высоты на основание.

Площадь круга

Площадь круга можно найти, зная его радиус или диаметр. Площадь круга равна произведению числа Пи на квадрат радиуса (или половину квадрата диаметра).

Площадь эллипса

Площадь эллипса можно найти, зная его большую и малую полуоси. Площадь эллипса равна произведению числа Пи на произведение большей и меньшей полуосей.

Площадь параллелограмма

Площадь параллелограмма можно найти, зная его высоту и основание. Площадь параллелограмма равна произведению его высоты на основание.

Площадь трапеции

Площадь трапеции можно найти, зная её высоту и сумму оснований. Площадь трапеции равна произведению её высоты на сумму оснований, деленную на два.

Площадь цилиндра

Площадь цилиндра можно найти, зная его высоту и радиус основания. Площадь цилиндра равна сумме площадей двух оснований и площади боковой поверхности, которая равна произведению числа Пи на диаметр основания умноженный на высоту.

Таким образом, для вычисления площади фигуры требуется знать некоторые характеристики этой фигуры, такие как длина, ширина, высота, радиус и т.д. Существуют разные формулы для нахождения площадей разных фигур, и зная эти формулы, можно легко ответить на вопрос о площади фигуры.

Видео:

Математика без Ху%!ни. Определенные интегралы, часть 3. Площадь фигуры.